Vraag en antwoord
Wat is de Powerfactor (pf)
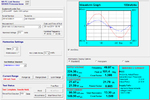 Wat is de Powerfactor van een armatuur
Wat is de Powerfactor van een armatuur
De Powerfactor, in het Nederlands genoemd de arbeidsfactor of vermogensfactor is de verhouding tussen werkelijk vermogen en schijnbaar vermogen in een wisselspannings-installatie en is eigenlijk het verschil tussen werkelijk vermogen (P) en het schijnbaar vermogen (S).
Het schijnbaar vermogen is het product van elektrische spanning (U) en elektrische stroom (I) en wordt uitgedrukt in VoltAmpère:
P(s) = U.I (VA)
Het werkelijk vermogen is de werkelijk overgebrachte hoeveelheid energie per tijdseenheid, in Watt:
P(w) = dE / dt (W)
In een gelijkstroominstallatie is het werkelijke vermogen gelijk aan stroom maal spanning, met andere woorden:
P(w) = U.I (W)
Bij een wisselspanning gaat dat niet altijd op. Ten gevolge van faseverschuiving tussen spanning en stroom, of door het niet sinusvormig zijn van spanning of stroom is er een afwijking.
Faseverschil (cos φ)
Als de stroom en de spanning (bij benadering) een sinus vorm hebben, wordt de arbeidsfactor bepaald door het faseverschil φ tussen de stroom en de spanning. Het werkelijke vermogen is dan gegeven als Pw = Ps |cos φ|. Dit is als volgt aan te tonen: stel dat de stroom als functie van de tijd gegeven wordt door I(t) = I0cos(ωt) en de spanning als V(t) = V0cos(ωt + φ), waar ω de hoekfrequentie van het signaal is, in rad / s. Dan is het schijnbare vermogen Ps = (1/2) V0 I0.
Dit is het werkelijke vermogen als de signalen precies in fase zijn. De factor 1/2 komt doordat I0 en V0 de piekwaarden zijn, en het vermogen door de effectieve waarde wordt bepaald.
Het werkelijke vermogen als functie van de tijd is nu Pw(t) = V(t)I(t) = V0I0cos(ωt)cos(ωt + φ).
Het werkelijke vermogen is nu het gemiddelde van dit vermogen als functie van de tijd. Daarvoor nemen we het gemiddelde over één periode van het signaal:
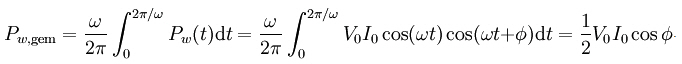
De arbeidsfactor is dus:
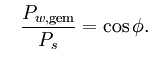
Hieruit volgt dat de arbeidsfactor nul is als de signalen 90° uit fase zijn.
Vervorming
Het bovenstaande geldt alleen als stroom en spanning precies sinus vormig zijn. Een andere oorzaak van een niet-ideale arbeidsfactor is de vervorming van het signaal. Wanneer stroom en spanning niet precies sinusvormig zijn en niet exact dezelfde vorm hebben, zal de arbeidsfactor ook kleiner dan 1 zijn. Doordat het signaal ook harmonischen bevat, kan er echter niet een duidelijk faseverschil φ worden gedefinieerd, en de "cos φ"-formule gaat niet zonder meer op.
Dit soort vervormingen kan optreden bij niet-lineaire belastingen, zoals gelijkrichters en omvormers.
Gevolgen
Het belangrijkste gevolg van een arbeidsfactor kleiner dan 1 is dat er meer elektrisch vermogen getransporteerd moet worden dan er nuttig opgenomen wordt. Dit leidt tot grotere transportverliezen in het lichtnet en het hoogspanningsnet. Om deze reden zijn er vaak eisen gesteld aan de arbeidsfactor van (grote) elektrische apparaten of wordt er Cos φ compensatie toegepast.
